Сторінка
2

Методи оцінювання ризиків на ринку цінних паперів

Фактор «бета» — це показник недиверсифікованого ризику, який демонструє, як реагує курс цінного папера на ринкові сили (чим більше, тим вищий фактор «бета» для цього цінного папера).

Фактор «бета» розраховують на основі взаємозв’язку фактичної дохідності цінних паперів і фактичної ринкової дохідності (остання зазвичай розраховується як середній показник дохідності всіх або великої кількості акцій). Фактор «бета» для всього фондового ринку дорівнює 1; усі інші його значення розглядаються відносно цієї величини. «Бета» може бути як додатнім, так і від’ємним, хоча майже всі значення цього по- казника зазвичай позитивні, і більшість акцій мають «бету» в діапазоні від 0,5 до 1,75.

На Заході основна частина брокерських фірм і видавництв фінансових видань публікує фактори «бета» для широкого спектра цінних паперів. Чим вищий фактор, тим більший ризик має цінний папір (табл. 11.8).

Таблиця 11.8

ВЗАЄМОЗВ’ЯЗОК ФАКТОРА «БЕТА» ТА РИЗИКУ

Отже, «бета» показує тип реакції цінного папера на дії ринкових сил. Наприклад, якщо очікується, що ринкові процеси призведуть до 100-процентного зростання ставки дохідності впродовж останнього періоду, тоді на акції зі значенням «бети» 1,5 очікувалось би збільшення доходу в цей період приблизно на 15 % (1,5 · 10 %).

Для акцій, у яких значення «бета» додатне, збільшення ринкової дохідності призводить до зростання дохідності цінних паперів. На жаль, зменшення ринкової дохідності зумовлює протилежну ситуацію. І в цьому полягає ризик. У попередньому прикладі, якщо очікується падіння ринкової дохід­ності на 10 %, то за акціями з «бетою» 1,5 очікується зменшення дохідності на 15 %. Оскільки фактор для цих акцій більший 1, то вони сильніше реагують, ніж ринок, маючи 15-процентне зниження своєї дохідності порівняно з 10-про­центним зменшенням дохідності ринкового портфеля. Акції, «бета» яких менший 1, звичайно, не будуть такими чутливими до змін ринкової дохідності. Відповідно, вони вважаються менш ризикованими.

Для того щоб формалізовано пов’язати поняття ризику й дохідності з фактором «бета», використовують модель оцінки капітальних активів (МОКА), розроблену американськими економістами У. Шарпом і Дж. Лінтером усередині 60-х років.

Фактор «бета» як показник недиверсифікованого ризику використовується в моделі для визначення очікуваної норми дохідності інвестицій відповідно до рівняння:

,

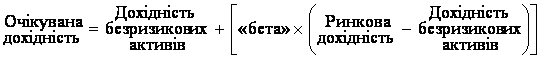де очікувана дохідність — це дохідність інвестицій за даного рівня ризику, який вимірюється за допомогою фактора «бета»;

ринкова дохідність — середня дохідність усіх цінних паперів;

дохідність безризикових активів — це дохідність, яку можна отримати на вільні від ризику інвестиції.

Потрібно зазначити, що очікувана дохідність зростає зі збільшенням фактора «бета».

Графічне відображення моделі оцінки капітальних активів називається кривою ринку цінних паперів (Cecurity Market Line — SML). Ця крива показує очікувану дохідність, яку бажав би отримати інвестор на ринку цінних паперів для кожного рівня недиверсифікованого ризику.

Модель можна побудувати, просто обчисливши очікувану дохідність для різних значень фактора «бета», залишаючи постійними ставку дохідності безризикових активів і ринкову дохідність. Наприклад, за ставки дохідності безризикових активів, що дорівнює 6 %, і ринкової дохідності в 10 % очікувана буде дорівнювати 11 %, якщо фактор «бета» дорівнює 1,25. Якщо збільшити його до 2, то дохідність становитиме 14 %. Аналогічно можна знайти її для різних значень «бета» та закінчити наступними комбінаціями ризику й очікуваної дохідності.

Наносячи ці величини на графік, можна отримати пряму лінію, яка показує, що зі збільшенням очікуваної дохідності ризик зростає (рис. 11.7).