Сторінка
2

Раціональні стратегії боротьби з корупцією

Далі було проведено оптимізацію моделі обмеження корупції.

Потрібно було знайти при якому розмірі штрафу С та при якій величині затрат на перевірки R, частка корумпованих агентів B(t) буде мінімальною.

Оскільки дана модель має вигляд об’єднання двох рівнянь, а наш графік (рис. 3.1.) складається з двох частин, то мінімум буде знаходитися в якійсь одній з цих частин, тобто він буде рішенням одного із двох рівнянь.

Можна побачити, що друге рівняння із об’єднання – рівняння

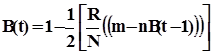
залежить лише від затрат на перевірки R, все інше нам відомо. Це рівняння не має мінімуму, оскільки

Отже мінімум знаходиться в першому рівнянні моделі:

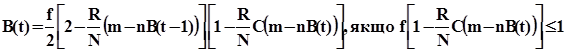
Мінімізація моделі була зроблена Методом Лагранжа.

Зміст методу Лагранжа полягає в тому, що спочатку складається функція Лагранжа, потім беруться похідні по всім невідомим змінним, які прирівнюються до 0. Тобто ми отримуємо систему трьох рівнянь з трьома невідомими, розв’язавши яку ми знайдемо наші невідомі змінні, і підставивши їх у початкову функцію, отримаємо мінімальне значення цієї функції.

Результати дослідження. Було зроблено припущення, що держава проводить перевірки бюрократів в кінці кожного кварталу. Потрібно було визначити, чи зменшиться і як частка корумпованих агентів на кінець року. Доля корумпованих агентів на початок першого кварталу – відома. Оскільки частка корумпованих агентів B(t) в період t залежить від частки корумпованих агентів B(t – 1) в період (t – 1) , це означає, що для того щоб знайти долю корумпованих агентів на кінець року треба пройти чотири періоди. Тобто t належить проміжку [1; 4].

Проте було враховано, ще такий параметр як граничне значення чесності бюрократів, оскільки воно також суттєво впливає на результат.

Розглянуто два припущення :

– перше, коли граничне значення чесності бюрократів (Н) не змінюється протягом року, тобто залишається таким яким воно було на початку;

– друге, коли на протязі року граничне значення чесності бюрократів (Н) змінюється.

Перше припущення.

Нехай Н = 0,554. Тоді, в результаті проведення перевірок в кінці третього кварталу можна побачити, що мінімальна частка корумпованих агентів в період t=3 співпадає із мінімальна частка корумпованих агентів в період t=2, тобто В(3) = В(2) = 0,597 або 59,7 %.Отже маємо стан рівноваги, при якому частка корумпованих агентів в даний період дорівнює частці корумпованих агентів за минулий період .

Тобто подальше проведення перевірок не призведе до зменшення частки корумпованих бюрократів, проте буде підтримувати її у рівноважному стані.

Залежність частки корумпованих агентів в часі можна побачити на графіку (рис. 1.2).

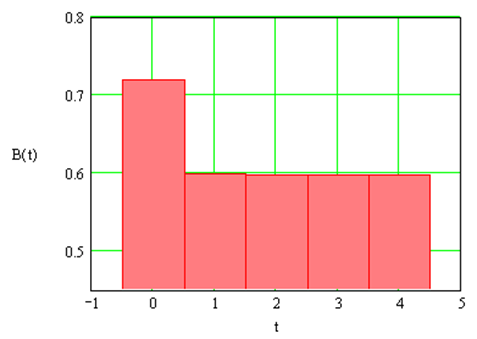
Рис. 1.2. Графік залежності частки корумпованих агентів В(t)від tпри Н = 0,554 .

Нехай Н = 0,574. В результаті проведення перевірок маємо стан рівноваги В(3) = В(2) = 0,559 або 55,9 %.Залежність частки корумпованих агентів в часі можна побачити на графіку (рис. 1.3).

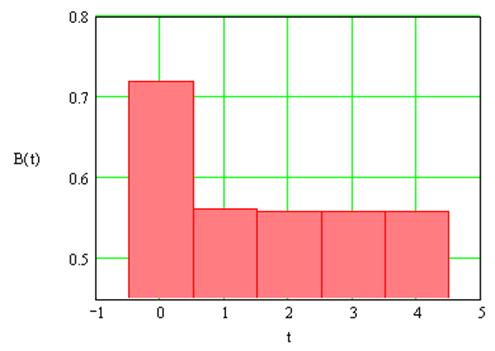
Рис. 1.3. Графік залежності частки корумпованих агентів В(t)від tпри Н = 0,574 .

Нехай Н = 0,599. В результаті проведення перевірок маємо стан рівноваги В(3) = В(2) = 0,494 або 49,4 %.Залежність частки корумпованих агентів в часі можна побачити на графіку (рис. 1.4).

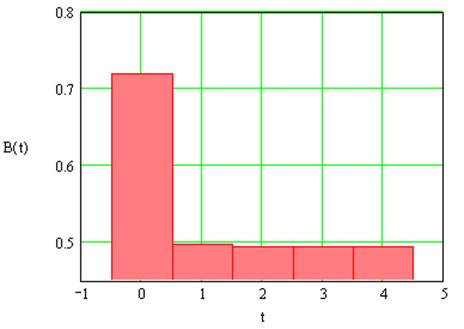
Рис. 1.4. Графік залежності частки корумпованих агентів В(t)від tпри Н = 0,599 .

Із графіків (рис. 1.2, 1.3, 1.4 ) витікає, що при збільшенні граничної чесності бюрократів мінімальне значення частки корумпованих агентів, яке ми шукаємо зменшується.

Друге припущення.

Нехай Н ≠ const , H Î [0,554; 0,599]. Залежність частки корумпованих агентів в часі можна побачити на графіку (рис. 1.5).

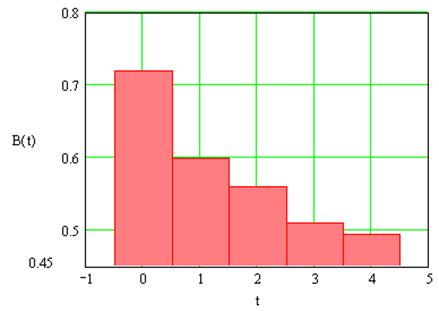
Рис. 1.5. Графік залежності частки корумпованих агентів В(t)від tпри Н ≠ const.

Із графіка витікає, що, потрохи збільшуючи в кожному кварталі граничне значення чесності бюрократів, значення частки корумпованих агентів з кожним кварталом буде зменшуватись.

Порівнюючи отримані результати мінімізації на основі двох припущень, видно, що при однакових початкових значеннях Н = 0,554, частка корумпованих агентів в кінці року різна. У випадку рис. 1.5 частка корумпованих агентів в кінці року становить 0,494, а у випадку рис. 1.2 – 0,597.

Це означає, що завданням держави є не тільки обмеження корупції, але і намагання, різними економічними, соціальними та політичними заходами, підвищувати граничне значення чесності своїх чиновників.

Також було розглянуто випадок, коли перевірки робилися не кожного кварталу, а раз на рік. За таких умов було отримано, що на кінець року частка корумпованих агентів склала 0,599. Хоча затрати на фінансування в даному випадку виявилися значно меншими, ніж при щоквартальній перевірці, проте частка корумпованих бюрократів виявилась більшою ніж в попередніх випадках. До того ж роблячи перевірки раз на рік держава б не враховувала можливість зміни граничного значення чесності бюрократів протягом цього року, що є дуже важливим як було видно з попереднього графіка, оскільки в тому випадку на кінець року частка корумпованих агентів становила 0, 494.

Тобто, проведення перевірок раз на рік є не вигідним для держави, оскільки принесе їй меншу вигоду, ніж щоквартальне проведення перевірок.

Висновки. Проведено оптимізацію моделі обмеження корупції та її практичну реалізацію.