Сторінка
2

Оцінювання дохідності операцій з фінансовими активами

Припустимо, що рівень інфляції за період t дорівнює і. Щоб забезпечити реальну дохідність операції обліку векселя на рівні, що визначався величиною kK, треба номінальну вартість векселя N скоригувати на множник (1 + і). Використовуючи формулу (13.29), отримаємо

З іншого боку, скориговану величину N1 можна подати у вигляді

де kk1 — ставка, що враховує інфляцію. Прирівнявши вирази (13.31), (13.32) та здійснивши деякі перетворення, отримаємо

де kKi — номінальна купонно-еквівалентна ставка доходу, яка забезпечує інвестору реальну дохідність на рівні kK при рівні інфляції за період і.

Аналогічно можна визначити облікову ставку &Б1, що компенсує інфляційні витрати і забезпечує реальну дохідність, яка визначається обліковою ставкою kE:

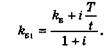
Приклад 4. Використавши дані, наведені в прикладі 1, визначити облікову ставку, яка компенсуватиме банку втрати від інфляції, якщо рівень інфляції і за період від дати обліку до дати погашення векселя (6 міс.) становив 10%. Облікову ставку з урахуванням інфляції визначимо на основі формули (13.34):

Приклад 5. Визначити необхідну ставку доходу за безпроцентною облігацією (див. приклад 3), яка б забезпечила реальну дохідність на рівні 8,65% при рівні інфляції за період з 01.04.02 р. по 01.09.02 р. — 20%. Необхідну ставку купонно-еквівалентного доходу, що зберігає реальну дохідність на рівні 8,65% в умовах інфляції, визначають за формулою (13.33)

Крім банківсько-дисконтної та купонно-еквівалентної ставки доходу, у фінансових розрахунках для визначення дохідності дисконтних боргових зобов'язань використовують також ефективну ставку доходу, яка визначається за формулою

Ринкова вартість дисконтного зобов'язання, що забезпечує необхідний рівень ефективного доходу ке, розраховується на основі формули (13.35)

Визначення дохідності операцій з купівлі-продажу процентних боргових зобов'язань та акцій базується на використанні формули (13.24) і може бути проілюстровано на таких прикладах.

Приклад 6. Інвестором було придбано 100 акцій за ціною 12,5 гр. од. за кожну. Через півроку вони були продані за ціною 15 гр. од. за акцію після сплати за ними дивідендів у розмірі 3 гр. од. на акцію. Визначити дохідність операції.

Використавши формулу (13.24), отримаємо

k = (15 - 12,5 + 3) 2 : 12,5 = 0,88, або 88%.

Прибуток, отриманий інвестором у грошовому вираженні, обчислимо за формулою

де п — кількість акцій; Рп — ціна продажу акцій; Рк — ціна купівлі; В — дивідендні виплати за період.

Приклад 7. Припустимо, що за три місяці до терміну погашення інвестором було придбано 10 купонних облігацій з купоном 15% за ринковою ціною 1105 гр. од. Через 3 міс. облігації були погашені за номінальною вартістю 1000 гр. од. кожна. Визначити дохідність операції.

Оскільки при погашенні сплачується не тільки номінальна вартість, а й купонний процент у сумі: 0,15 • 1000 = 150 гр. од., дохідність операції на основі формули (13.24)

Прибуток, обчислений за формулою, аналогічною (13.37),

П = 10 (1000 - 1105 + 150) = 450 гр. од.

Рекомендована література

1. Брігхем Є.Ф. Основи фінансового менеджменту. — К.: Молодь, 1997.

2. Панова С. Анализ финансового состояния коммерческого банка. — М.: Перспектива, 1996.

3. Финансовое управление компанией / Под ред. Е.В. Кузнецовой. — М.: Фонд "Правовая культура", 1996.

4. Шарп У., Александер Г., Бэйли Дж. Инвестиции: Пер. с англ. — М.: ИНФРА-М, 1997.

5. Fabozzi J Modigliani E. Capital markets: institutions and instruments. — Prentice Hall Inc., 1996.

6. Livingston M. Money and capital markets. — Prentice Hall Inc., 1990.